
See materjal on loodud Tiigrihüppe Sihtasutuse programmi ProgeTiiger raames.
Ülesande eesmärk
Ehitada ja programmeerida robot, mis suudab ekraanile kuvada oma läbitud teekonna.
Käesoleva ülesande lahendamine kestab 2 robootika tundi, kusjuures ühe tunni pikkuseks on arvestatud 2x45 min.
Ülesande lahendamiseks vajalik
Õpilased peavad olema hästi kursis matemaatikaga ja oskama arvutada täisnurkse kolmnurga külgede pikkuseid nii koosinuse kui ka siinuse abil.
Õpilane peab arvesse võtma ülesande lahendamisel järgmisi asjaolusid:
1) Ratta läbimõõt
2) Rataste teljevahe
3) Peab oskama tuletada roboti pöördenurga, kui ülejäänud muutujad on teada
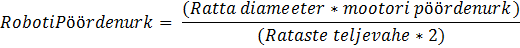
4) Peab oskama arvutada kolmnurga lähiskaateti pikkust tervanurga ning hüpotenuusi abil
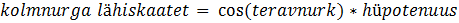
5) Peab oskama arvutada vastaskaateti pikkust teravnurga ning hüpotenuusi abil
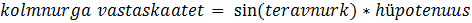
6) Peab oskama aru saada NXT koordinaatteljestikust, mis on mõõtudega 100x64 pikselit
Ülesande lahendamise käik
Lahenduse koodi pole mõttekas õpilastele ette anda, tegemist on nii lihtsa koodiga, et selle mahakirjutamine võtaks aega 10 min, kuid tarkus jääks tulemata.
Ülesanne on jaotatud neljaks etapiks mille käigus õpilased jõuavad järk-järgult lahenduseni.
Etapid ja õppetundide jaotus:
1. Tund
a. Roboti pöördenurga leidmine rataste pöördenurga abil
b. Kolmnurga lahendamine, lähis- ja vastaskaatetite leidmine (siinus, koosiinus)
2. Tund
a. Roboti pöördenurk ning kolmnurga lahendamine kokku pandud (suunamõõdik ekraanil)
b. Lõplik ülesande lahendus
Roboti pöördenurga leidmine
Selle etapi eesmärk on lasta õpilastel jõuda valemini, mille abil saab teisendada roboti rattakeeramise kraadid roboti enda pööramise kraadideks. See on vajalik, kuna ülesande lahendus baseerub omadusel, et meil on teada igal hetkel rataste omavahelise pöördenurga vahe.
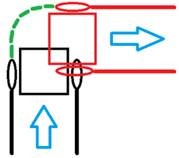
Kõige lihtsam on tuua näide seisva robotiga, kus meil on teada et üks ratas seisab ja teine ratas pöörab näiteks 360 kraadi, ehk teeb ühe tiiru. Sellisel juhul saame roboti pöördenurgaks 90 kraadi, eeldusel et rataste teljevahe on 110 mm ja diameeter 56 mm.
Õpilased on varasemalt lahendanud ülesandeid, mille käigus nad on pidanud vastupidist ülesannet lahendama, st. et on teada mitu kraadi peab robot pöörama ning õpilased peavad välja arvutama mitu kraadi peab ratas pöörama, et saavutada roboti õige positsioon.
Õpilased on siiani kasutanud valemit:
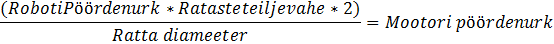
Käesoleva ülesande käigus peavad õpilased algatuseks avaldama valemist RobotiPöördenurga.
Kui neil on valem õigesti avaldatud, kirjutavad nad programmi, mille abil saab kuvada roboti pöördenurga ekraanile numbriliselt. See annab neile kohest tagasisidet, kas nad on õigesti avaldanud RobotiPöördenurga ning seda ka õigesti rakendada oskavad.
Antud etapi lahendus on alljärgnev programmikood.
//käesolev programm kuvab ekraanil roboti pöördenurga
//roboti mootorite pöörete järgi arvutatakse välja roboti pöördenurk
//ja kuvatakse see ekraanil
//testimiseks tuleb robotit käsitsi liigutada.
//Roboti pööramise nurk = (Diameeter * x kraadi)/(Rataste vahe * 2)
task main()
{
int RattaDiameeter = 56; //ratta diameeter
int RatasteVahe = 110; //ratastevaheline kaugus, teljevahe
int suund; //mootori pöörete vahe
float BMootor; //mootori B pöörded
float CMootor; //mootori C pöörded
int RobotiNurk; //roboti pööramise nurk
while (1)
{
//mootorite pöörded loetakse muutujatesse
BMootor = MotorRotationCount(OUT_B);
CMootor = MotorRotationCount(OUT_C);
//lahutatakse ühe mootori pöördenurgast teise mootori pöördenurk
//tulemuseks on ratastevaheline erinevaus pöördenurgas
suund = BMootor - CMootor;
//siin arvutatakse välja roboti pöördenurk, võttes arvesse rataste läbimõõtu
//rataste teljevahe ja ratastevaheline kraadide erinevus
RobotiNurk = (RattaDiameeter * suund)/(RatasteVahe * 2);
ClearLine(LCD_LINE1);
//ekraani ülemisel real kuvatakse roboti nurk
NumOut(0, LCD_LINE1, RobotiNurk);
TextOut(30, LCD_LINE1, "kraadi");
}
}
Kolmnurga lahendamine
Selle etapi eesmärk on lasta õpilastel lahendada kolmnurk, mille kohta on teada üks teravnurk ning hüpotenuus. Leida on tarvis lähiskaateti ja vastaskaateti pikkused.
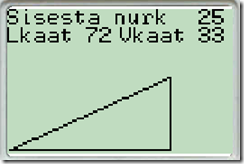 Lahendatud kolmnurk tuleb kuvada ekraanil ning peab olema muutumises koos nurga muutmisega. Nurga muutmine teostada noolenuppudega parem-vasak, sammuga 5 kraadi.
Lahendatud kolmnurk tuleb kuvada ekraanil ning peab olema muutumises koos nurga muutmisega. Nurga muutmine teostada noolenuppudega parem-vasak, sammuga 5 kraadi.
Antud etapp on olulise tähtsusega, kuna selle abil jõuavad õpilased ülesande lõpuks äratundmisele, kuidas aitab kolmnurga lahendamine neid robootika liikumisülesande juures teekonna kuvamisel. Neil peaks tekkima side matemaatika õppimise vajaduse ja reaalse elu vahel.
Kolmnurga lähis- ja vastaskaateti pikkuste arvutamise valemid. Vaata joonist.
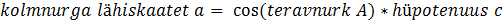
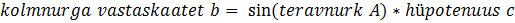
Kui nad on kolmnurga lahendamisest aru saanud, tuleb selle kohta programm kirjutada. Programm võiks välja näha selline, et hüpotenuus on ette antud (ülesande lahenduses on see samuti mittemuutuv suurus), kuid nurka peab saama muuta ja tulemusena kuvatakse ekraanil kolmnurga lähis- ja vastaskaatetite pikkused.
Kolmnurga lahendamise programmikood.
//käesolev programm lahendab kolmnurga
//ja joonistab selle ekraanile
//lähiskaatet = teravnurga koosinu * hüpotenuus
//vastaskaatet = teravnurga siinus * hüpotenuus
task main()
{
int RobotiNurk=45; //roboti pööramise nurk
int Lkaatet; //lähiskaatet
int Vkaatet; //vastaskaatet
int Hypotenuus=80; //hüpotenuus
while (1)
{
ClearScreen();
TextOut(0, LCD_LINE1, "Sisesta nurk");
NumOut(85, LCD_LINE1, RobotiNurk);
if(ButtonPressed(BTNCENTER, FALSE))
{
while(ButtonPressed(BTNCENTER, FALSE));
break;
}
if(ButtonPressed(BTNRIGHT, FALSE))
RobotiNurk += 5;
while(ButtonPressed(BTNRIGHT, FALSE));
if(ButtonPressed(BTNLEFT, FALSE))
RobotiNurk -= 5;
while(ButtonPressed(BTNLEFT, FALSE));
//arvutatakse välja lähiskaateti pikkus
Lkaatet = cosd(RobotiNurk) * Hypotenuus;
//arvutatakse välja vastaskaateti pikkus
Vkaatet = sind(RobotiNurk) * Hypotenuus;
TextOut(0, LCD_LINE2, "Lkaat");
TextOut(50, LCD_LINE2, "Vkaat");
NumOut(35,LCD_LINE2, Lkaatet);
NumOut(85,LCD_LINE2, Vkaatet);
//ekraanile joonistatakse lähiskaatet
LineOut(1, 1, Lkaatet, 1);
//ekraanile joonistatakse vastaskaatet
LineOut(Lkaatet, 1, Lkaatet, Vkaatet);
//ekraanile joonistatakse hüpotenuus
LineOut(1, 1, Lkaatet, Vkaatet);
Wait(100);
}
}
Roboti liikumise suunanäidik
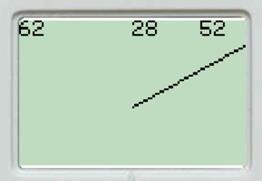 Selle etapi eesmärk on panna kokku esimene ja teine etapp, ehk siis ühendada omavahel roboti pöördenurga arvutamine ja kolmnurga lahendamine.
Selle etapi eesmärk on panna kokku esimene ja teine etapp, ehk siis ühendada omavahel roboti pöördenurga arvutamine ja kolmnurga lahendamine.
Etapi lõpptulemusena valmib NXT ekraanile suunanäidik, mis näitab suunda kuhu poole robot sõidab. Seda omadust kasutame lõpplahenduses roboti teekonna kuvamiseks.
Roboti suunanäitamise programmi kood.
//käesolev programm kuvab ekraanile roboti liikumise suuna
//Roboti pööramise nurk = (Diameeter * x kraadi)/(Rataste vahe * 2)
//lähiskaatet = teravnurga koosinu * hüpotenuus
//vastaskaatet = teravnurga siinus * hüpotenuus
task main()
{
int RattaDiameeter = 56; //ratta diameeter
int RatasteVahe = 110; //ratastevaheline kaugus, teljevahe
int suund; //mootori pöörete vahe
float BMootor; //mootori B pöörded
float CMootor; //mootori C pöörded
int RobotiNurk; //roboti pööramise nurk
int Lkaatet; //lähiskaatet
int Vkaatet; //vastaskaatet
int Hypotenuus=60; //hüpotenuus
while (1)
{
//mootorite pöörded loetakse muutujatesse
BMootor = MotorRotationCount(OUT_B);
CMootor = MotorRotationCount(OUT_C);
suund = BMootor - CMootor;
//siin arvutatakse välja roboti pöördenurk, võttes arvesse rataste läbimõõtu
//rataste teljevahe ja ratastevaheline kraadide erinevus
RobotiNurk = (RattaDiameeter * suund)/(RatasteVahe * 2);
//arvutatakse välja lähiskaateti pikkus
Lkaatet = cosd(RobotiNurk) * Hypotenuus;
//arvutatakse välja vastaskaateti pikkus
Vkaatet = sind(RobotiNurk) * Hypotenuus;
ClearScreen();
//ekraanile joonistatakse roboti suunanäidik
LineOut(50, 25, Vkaatet+50, Lkaatet+25);
//ekraani ülemisel real kuvatakse roboti nurk ning lähis- ja vastaskaatet
NumOut(0, LCD_LINE1, RobotiNurk);
NumOut(50,LCD_LINE1, Lkaatet);
NumOut(80,LCD_LINE1, Vkaatet);
Wait(100);
}
}
Lõplik ülesande lahendus
Alljärgnevalt roboti teekonna kaardistamise programmi kommenteeritud kood.
Sisuliselt tekib ekraanile joon hästi paljude pisikeste kolmnurkade lahendamise tulemusena.
Siin on lisandunud eelkirjeldatud etappidega võrreldes kaks olulist võtet.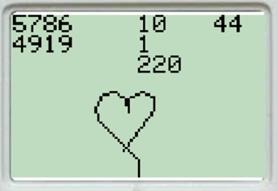
1. Kaardistamise sageduseks kasutatakse rataste pöörlemist. Kui ükskõik kumb ratas teeb 360 kraadi, ehk ühe täisringi, arvutatakse ja salvestatakse selle hetke roboti olukord ekraanil. See võte on vajalik eelkõige seetõttu, et robot ei suuda ühe rattapöörde jooksul kuigi palju viga teha ning see on piisav et saada küllaltki täpne joon ekraanil. Alati võib proovida ise selle täpsust suurendada, vähendades roboti rataste kraadide arvu mille jooksul toimub kaardistamine.
2. Kolmnurga hüpotenuusi seadmine. See võimaldab muuta ekraanile kujutatava joone pikkust ja täpsust. Kui hüpotenuus panna liiga lühike, näiteks 2 punkti, siis on kaatetite tulemuseks ainult 1 või 0 ning joone täpsus kannatab olulisel määral. Kui aga hüpotenuus panna liiga pikk, joonistatakse ekraanile korraga väga pikk joon, mis on samuti mõttetu ekraani väikse pinna tõttu.
Ekraanipilt antud programmi tulemusest NXT ekraanil.
//käesolev programm on roboti teekonna kaardistaja
//roboti mootorite pöörete järgi arvutatakse välja roboti teekonna kaart
//ja kuvatakse see ekraanil
//task soida on lihtsalt roboti sõitmise ja kaardistamise testimiseks
//task sõida abil sõidab robot südame kujutise ning joonistab selle ka ekraanile
task soida()
{
while(1)
{
RotateMotorEx(OUT_BC, 40, 360, 0, TRUE, TRUE);
RotateMotorEx(OUT_BC, 40, 360, 15, TRUE, TRUE);
RotateMotorEx(OUT_BC, 40, 1300, 0, TRUE, TRUE);
RotateMotorEx(OUT_BC, 40, 1600, -20, TRUE, TRUE);
RotateMotorEx(OUT_BC, 40, 370, 100, TRUE, TRUE);
RotateMotorEx(OUT_BC, 40, 1400, -25, TRUE, TRUE);
RotateMotorEx(OUT_BC, 40, 1300, 0, TRUE, TRUE);
//sõidu lõppedes oodatakse kuni nuppu vajutatakse
while(!ButtonPressed(BTNCENTER, FALSE));
}
}
//siin paar abivalemit, mille alusel arvutatakse roboti teekonna kaart
//Roboti pööramise nurk = (Diameeter * x kraadi)/(Rataste vahe * 2)
//lähiskaatet = teravnurga koosinus * hüpotenuus
//vastaskaatet = teravnurga siinus * hüpotenuus
task main()
{
int RattaDiameeter = 56; //ratta diameeter
int RatasteVahe = 110; //ratastevaheline kaugus, teljevahe
int suund; //mootori pöörete vahe
float BMootor; //mootori B pöörded
float CMootor; //mootori C pöörded
float LastBMootor;
float LastCMootor;
int RobotiNurk; //roboti pööramise nurk
int Lkaatet=0; //lähiskaatet
int Vkaatet=50; //vastaskaatet
int xLkaatet;
int xVkaatet;
int Hypotenuus=6; //hüpotenuus, selle numbri ja nurga põhjal arvutatakse välja Lähis- ja Vastaskaatet
StartTask(soida);
while (1)
{
//mootorite pöörded loetakse muutujatesse
BMootor = MotorRotationCount(OUT_B);
CMootor = MotorRotationCount(OUT_C);
//antud if lause tingimus on võte, millega tagatakse kaardistamise sagedus
//1 rattapööre = 1 joonistus ekraanil
//seega antud if lause käivitub alles siis, kui B või C Mootor on teinud 360 kraadi
if (BMootor > LastBMootor+360 || CMootor > LastCMootor + 360)
{
LastBMootor = BMootor;
LastCMootor = CMootor;
suund = BMootor - CMootor;
//siin arvutatakse välja roboti pöördenurk, võttes arvesse rataste läbimõõtu
//rataste teljevahe ja ratastevaheline kraadide erinevus
RobotiNurk = (RattaDiameeter * suund)/(RatasteVahe * 2);
//eelmise tsükli käigus saadud lähis- ja vastaskaatet salvestatakse ajutisse muutujasse
//selle alusel määratakse ekraanil joone alguspunkt
xLkaatet = Lkaatet;
xVkaatet = Vkaatet;
//arvutatakse välja lähiskaateti pikkus
Lkaatet = cosd(RobotiNurk) * Hypotenuus;
//arvutatakse välja vastaskaateti pikkus
Vkaatet = sind(RobotiNurk) * Hypotenuus;
//välja arvutatud lähis- ja vastaskaatetile liidetakse juurde nende
//eelmise tsükli tulemus, et tagada joone jätkumine samast punktist
//kus eelmise tsükli aja lõpetati
Vkaatet += xVkaatet;
Lkaatet += xLkaatet;
//kui kaatetid omandavad väärtuse mis on ekraani piirdeist väljas
//siis korrigeeritakse numbreid selliselt, et joon jätkuks ekraani vastasservast
if (Vkaatet>100)
{
Vkaatet = 1;
xVkaatet = 1;
}
if (Vkaatet<1)
{
Vkaatet = 100;
xVkaatet = 100;
}
if (Lkaatet>48)
{
Lkaatet = 1;
xLkaatet = 1;
}
if (Lkaatet<1)
{
Lkaatet = 48;
xLkaatet = 48;
}
//ekraanile joonistatakse roboti teekonna joon
LineOut(xVkaatet, xLkaatet, Vkaatet, Lkaatet);
ClearLine(LCD_LINE1);
//ekraani ülemisel real kuvatakse roboti nurk ning lähis- ja vastaskaatet
NumOut(0, LCD_LINE1, RobotiNurk);
NumOut(50,LCD_LINE1, Lkaatet);
NumOut(80,LCD_LINE1, Vkaatet);
}
}
}